Cepat dan Mudah Mengkonversi Biner ke Oktal , Desimal , dan Hexadesimal

Mengkonversi Sistem Bilangan Biner

 

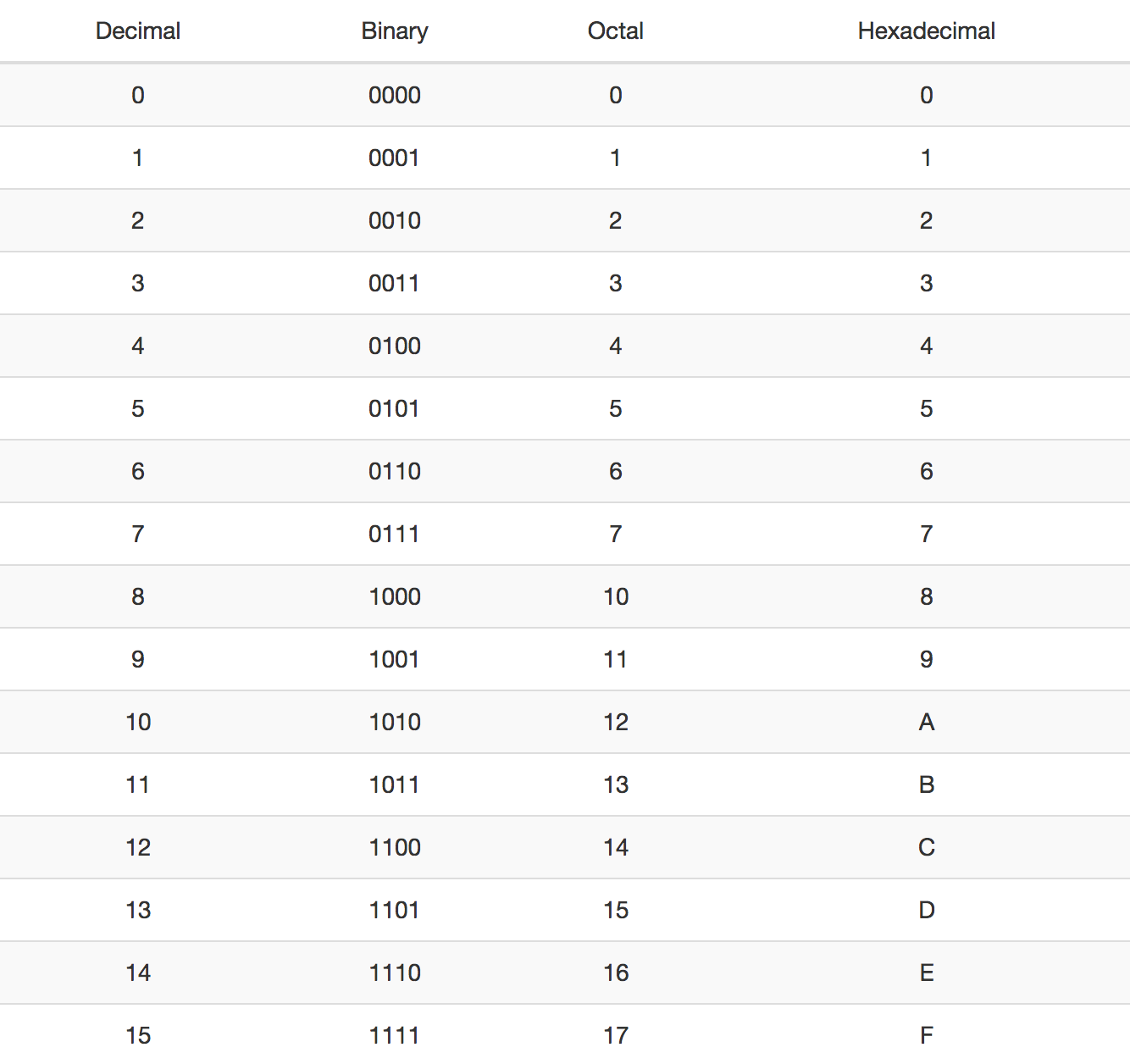
Ada baiknya kita mengetahui tabel ASCII diatas sebagai pedoman untuk mengubah biner ke oktal dan hexadesimal secara lebih mudah .

1.  Mengkonversi dari bilangan biner

110110111_{(2)= .........(8)...........(10)...........(16)}

1.1  Biner Ke Oktal (radiks 2 ke radiks 8)

Ambil 3 bagian per tim dari bilangan biner untuk dijadikan oktal yang dibagi per 3 mulai dari belakang

Contoh 1 :

110110111 = 110   110   11

Dengan melihat tabel ASCII Di atas halaman ini bisa kita ketahui bahwa ;

110₂ =6 , 110₂=6 ,111₂=7

Maka  110110111₂=667₈

Contoh 2 :

1010001110₂ = 1  010  001  110 = 1 2 1 6₈

 kenapa sih 111 = 7 ?

karena sesuai perhitungan dari postingan saya sebelumnya . karena biner radiks 2 oleh itu dikali 2 .maka kita mulai dari kanan 

1x2⁰ +1x2¹+ 1x2² =1+2+4 = 7

2.  biner ke desimal ( radiks 2 ke radiks 10 )

tinggal kita kalikan saja dari yang paling kanan ke paling kiri dengan 2⁰ sampai seterusnya

Contoh 1 : 

1 1 0 1 1 0 1 1 1

1x2⁰+1x2¹+1x2²+0x2³+1x2⁴+1x2⁵+0x2⁶+1x2⁷+1x2⁸=

1+2+4+0+16+32+0+128+256 = 439₁₀

3.  Biner ke Hexadesimal (radiks 2 ke radiks 16 )

caranya hampir sama dengan biner ke oktal . namun di hexa dibagi perbagian adalah 4 .dimana dibaginya mulai dari kanan .

110110111 = 1  1011  0111 = 1 B 7 ₁₆

kenapa 1011 = B ?

karena 1011 = 1x2⁰+1x2¹+1x0²+1x2³= 1+2+8 = 11

kenapa sih 11 jadi B ? 

karena !

biner memiliki 16 anggota yaitu (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)

dimana A=10 ,B=11 ,C=12 ,D=13 ,E=14 ,F=15

Klik Disini jika ingin ke postingan sebelumnya

Anda bertanya di komentar , saya akan jawab